マハラノビス距離
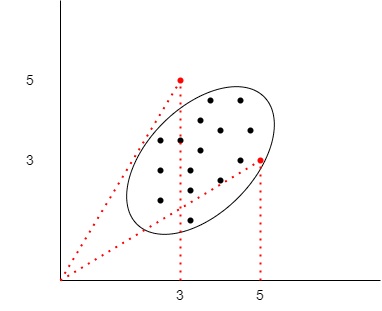
マハラノビス距離は、多変数間の相関関係を考慮した距離のこと。例えば、下記の図の赤の2点はユークリッド距離で考えると両方同じ距離となる。しかし、相関関係のある集団から見てみると右側の赤の点は集団に属しているのに対し、左側の赤の点は集団からはみ出している。このように、相関関係を考慮して考えることで、異常な値を見つけることができる。
ベクトルx : \(\displaystyle x = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) \)
ベクトルy : \(\displaystyle y = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right) \)
マハラノビス距離(1) : \(\displaystyle d(x, y) = \sqrt{(x – y)^{T \sum^-1} + (x – y)} \)
\(\displaystyle \sum \)は、共分散の行列を表している。また、\(\displaystyle \sigma_{mn} \)は\(\displaystyle m \)と\(\displaystyle n \)の共分散、\(\displaystyle \sigma_{n}^2 \)は\(\displaystyle n \)の分散を表している。\(\displaystyle \sum \)が共分散の行列を表しているのにも関わらず、分散\(\displaystyle n \)が出てくるのは、同じ次元の共分散は分散となるから。共分散と分散の公式を見てみるとわかる。
マハラノビス距離(2) : \(\displaystyle \begin{eqnarray} \sum = \left( \begin{array}{cccc} \sigma_{1}^{2} & \sigma_{ 12 } & \ldots & \sigma_{ 1n } \\ \sigma_{ 21 } & \sigma_{ 2 }^{2} & \ldots & \sigma_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{n1} & \sigma_{n2} & \ldots & \sigma_{n}^{2} \end{array} \right) \end{eqnarray} \)
分散 : \(\displaystyle \sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2 \)
共分散 : \(\displaystyle \sigma_{x, y} = \frac{1}{n} \sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y}) \)
マハラノビス距離を相関関係から考えてみる。
標準偏差x : \(\displaystyle \sigma_x = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2} \)
標準偏差y : \(\displaystyle \sigma_y = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i – \bar{y})^2} \)
相関関係 : \(\displaystyle r = \frac{ \frac{1}{n} \sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y}) }{ \sqrt{\sum_{i=1}^n (x_i – \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i – \bar{y})^2} } = \frac{\sigma_{x, y}}{\sigma_x \sigma_y}\)
次のような2次元で考える。
\(\displaystyle \sum = \begin{pmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{pmatrix} = \begin{pmatrix} \sigma_{1}^{2} & \sigma_{12} \\ \sigma_{21} & \sigma_{2}^{2} \end{pmatrix} \)
まず、仮に平均が0の場合、分散の式から考えると1となる。
\(\displaystyle \sigma_{1}^{2} = \sigma_{2}^{2} = 1 \)
また、相関関係は下記の式から
\(\displaystyle r = \sigma_{12} = \sigma_{21} \)
よって、共分散の行列は次のようになる。
\(\displaystyle \sum = \begin{pmatrix} 1 & r \\ r & 1 \end{pmatrix} \)
ここで、マハラノビス距離の公式(1)に、 \(\displaystyle X = x_1 – x_2 \)、\(\displaystyle Y = y_1 – y_2 \)として代入する。
\(\displaystyle d(X, Y) = \sqrt{(X, Y) \begin{pmatrix} 1 & r \\ r & 1 \end{pmatrix}^{-1} \begin{pmatrix} X \\ Y \end{pmatrix}} = \sqrt{\frac{X^2 – 2rXY + Y^2}{1 – r^2}}\)
相関関係rは-1から1の範囲をとるので、rが1または-1へ近づいていくほど、マハラノビス距離が小さくなっていくことがわかる。
Pythonでマハラノビス距離を求める
NBA選手の身長と体重でマハラノビス距離を求めてみる。データセットはKaggleから頂いた(2021-22 NBA Season Active NBA Players)。Muhammet Ali Büyüknacarさん、ありがとうございます。
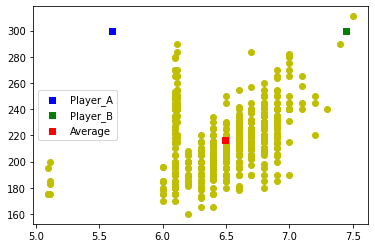
このNBA選手の集団に5.6フィート、200ポンドのPlayer_Aと7.45フィート、300ポンドのPlayer_Bを加え、それぞれユークリッド距離とマハラノビス距離を求めてみる。また、散布図にプロットしてみる。
import numpy as np
import pandas as pd
from scipy.spatial.distance import euclidean
from matplotlib import pylab as plt
players = pd.read_csv('データセットのcsvのパス')
# 共分散
cov = np.cov(players['Height_i'], players['Weight'])
# 共分散の配列
cov_mtr = np.array([
[cov[1][1], -cov[0][1]],[-cov[1][0], cov[0][0]]]) / \
(cov[0][0] * cov[1][1] - cov[0][1] * cov[1][0])
def mahalanobis(x, y, cov_mtr):
# マハラノビス距離
d = np.sqrt((x - y).dot(cov_mtr).dot((x - y).T))
return d
# 選手AとB
player_a = np.array([5.6, 300])
player_b = np.array([7.45, 300])
# 平均値
avg = np.array([np.mean(players['Height_i']), np.mean(players['Weight'])])
# 共分散
players_cov = np.cov(players['Height_i'], players['Weight'])[0][1]
print(players_cov)
result = pd.DataFrame([[euclidean(avg, player_a), mahalanobis(avg, player_a, cov_mtr)],
[euclidean(avg, player_b), mahalanobis(avg, player_b, cov_mtr)]],
index=['player_a', 'player_b'], columns=['euclidean', 'mahalanobis'])
print(result)
# グラフ描画
plt.scatter(players['Height_i'], players['Weight'], c='y')
plt.scatter(player_a[0], player_a[1], c='b', marker='s', label='Player_A')
plt.scatter(player_b[0], player_b[1], c='g', marker='s', label='Player_B')
plt.scatter(avg[0], avg[1], c='r', marker='s', label='Average')
plt.legend()2.5819287272446494| ユークリッド距離 | マハラノビス距離 | |
|---|---|---|
| Player_A | 83.841664 | 5.205281 |
| Player_B | 83.842389 | 3.897389 |
Player_AもBもユークリッド距離に関してはほぼ同じだが、マハラノビス距離に関してはPlayer_Aの方が離れている。グラフで見てみると、確かにPlayer_AはNBAの選手の中では身長と体重の傾向から逸脱していることがわかる。Player_Bの方は、身長が増えれば体重も増えるという相関には当てはまっている感じ。
scipyでのマハラノビス距離
scipyでは、mahalanobis関数で実装することができる。また、numpyではinv関数で逆行列を求めることができる。
from scipy.spatial.distance import mahalanobis
import numpy as np
import pandas as pd
players = pd.read_csv('/content/drive/MyDrive/nba_players.csv')
# 共分散
cov = np.cov(players['Height_i'], players['Weight'])
# 選手AとB
player_a = np.array([5.6, 300])
player_b = np.array([7.45, 300])
# 平均値
avg = np.array([np.mean(players['Height_i']), np.mean(players['Weight'])])
result1 = mahalanobis(avg, player_a, np.linalg.inv(cov))
result2 = mahalanobis(avg, player_b, np.linalg.inv(cov))
print(result1)
print(result2)5.205281064889013
3.8973885661017627同じ結果が出力された。

記事を読んでいただきありがとうございました。