期待値
期待値は、1回の試行した時に得られる値の平均値のことで、得ることができる値の全てと、それが起こる確率の乗算を足し合わせていったものです。\(\displaystyle x_i \)は確率変数、\(\displaystyle p_i \)は確率変数の確率です。
期待値 : \(\displaystyle \mu = \sum_{ i = 1 }^n x_i p_i \)
Pythonで期待値を求める
期待値の例として宝くじがよく使われているので、ドリームジャンボの当せん金の期待値を求めてみる。
| 等級等 | 当せん金 | 本数(12ユニット[1ユニット:1,000万枚]) |
| 1等 | 300,000,000円 | 12本 |
| 1等の前後賞 | 100,000,000円 | 24本 |
| 1等の組違い賞 | 100,000円 | 1,188本 |
| 2等 | 10,000,000円 | 24本 |
| 3等 | 1,000,000円 | 840本 |
| 4等 | 10,000円 | 360,000本 |
| 5等 | 3,000円 | 1,200,000本 |
| 6等 | 300円 | 12,000,000本 |
宝くじは「組」と「番号」で構成されていて、番号の集まりのことを「1ユニット」している。
期待値 : \(\displaystyle \mu = \sum_{ i = 1 }^n x_i p_i \)
# 当せん金の金額
money = [300000000, 100000000, 100000, 10000000, 1000000, 10000, 3000, 300]
# 各当せん金の本数
num = [12, 24, 1188, 24, 840, 360000, 1200000, 12000000]
# 合計本数(12ユニット * 1,000万枚)
total = 12 * 10000000
ev = 0
for m, n in zip(money, num):
ev += m * (n / total)
print(ev)149.99結果は約150円と宝くじの価格300円にも満たない。つまり、損する可能性が高いということです。
大数の法則
ある試行を極限まで繰り返していくと、平均値が期待値に収束していくという法則。つまり、一見偶然に見えるような事象も、大量に試行していくと、その事象に規則性があることがわかる。例えば、サイコロを振って「1の目」が出る確率は、振る回数を増やせば増やすほど\(\displaystyle \frac{1}{6} \)に近づいていく。
\(\displaystyle \bar{x} \)は標本平均のことで、\(\displaystyle \mu \)は期待値です。また、\(\displaystyle n \)が試行回数となります。
大数の法則(強) : \(\displaystyle Pr(\lim_{n \to \infty} \bar{x} = \mu ) \)
\(\displaystyle | \bar{x} – \mu| \)とすることで絶対値を取ります。
大数の法則(弱) : \(\displaystyle \lim_{n \to \infty} Pr(| \bar{x} – \mu| < \epsilon ) = 1 \)
Pythonで大数の法則を求める
6面あるサイコロで試してみる。まずは、サイコロを転がした時の期待値を求めてみる。宝くじの時は、本数が複数あったが、サイコロの場合は1個で考えるので確率変数\(\displaystyle p_i \)は\(\displaystyle \frac{1}{6} \)です。
大数の法則(強) : \(\displaystyle Pr(\lim_{n \to \infty} \bar{x} = \mu ) \)
# サイコロの面の値
num = [1, 2, 3, 4, 5, 6]
# 期待値
ev = 0
for i in num:
# 確率変数は1/6
ev += i * (1 / 6)
print(ev)3.5大数の法則で考えると、試行回数が増えれば増えるほど、出た目の標本平均はこの3.5へ近づいていく。つまり、標本平均(\(\displaystyle \bar{x} \))と期待される平均値(\(\displaystyle \mu \))が等しくなるということです。
import numpy as np
from matplotlib import pylab as plt
# 平均値
m = list()
# サイコロを振って出た目
n = np.array(list())
# 1から6までの数をランダムに1000回繰り返す
for i in np.random.choice(range(1, 7), size=1000):
# 配列にランダムな数を追加していく
n = np.append(n, i)
# 平均値を算出
m.append(n.mean())
# グラフを描画
plt.plot(m)
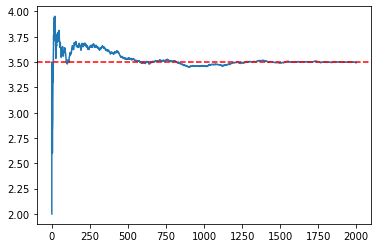
plt.axhline(y=3.5, color='r', linestyle='--')出力されたグラフを見てみると、3.5に収束していっているのがわかる。ランダムな値を取っているので試行する度にグラフは多少変化するが、必ず3.5に収束していく。
次は10のべき乗で変化を見てみる。
import pandas as pd
# DataFrameのインデックス
index = list()
# 平均値のデータ
data = {'平均値': list()}
# 10の1乗(10)から8乗(100000000)を繰り返す
for i in range(8):
n = 10 ** (i + 1)
index.append(n)
# 平均値を求める
data['平均値'].append(np.random.choice(range(1, 7), size=n).mean())
pd.DataFrame(data, index=index)出力されたDataFrameを見てみると試行回数が増えるに従い3.5に近づいていっていることがわかる。
| 平均値 | |
|---|---|
| 10 | 3.200000 |
| 100 | 3.330000 |
| 1000 | 3.561000 |
| 10000 | 3.514800 |
| 100000 | 3.493690 |
| 1000000 | 3.497537 |
| 10000000 | 3.499812 |
| 100000000 | 3.500019 |

記事を読んでいただきありがとうございました。