ネイピア数

ネイピア数は、無理数であり、自然対数の底(\(\displaystyle e \))と言われている数。もっと奥の深い数ではあるが、感覚の掴みにくい数なので、詳細な説明は省略する。

よく例に挙げられるのが、連続複利の元利合計です。元金１円を年利1(100%増えるといこと)、付利期間を1/n 年とし、1年預金した場合、1/n 年毎に利子1/n で元利合計が増えていくと次の式のようになる。

\(\displaystyle (1 + \frac{1}{n})^n \)

\(\displaystyle n = 1 \)　の場合は、1年後に100%増える。

　\(\displaystyle (1 + \frac{1}{1})^1 \)　→　\(\displaystyle 1 + 1 = 2 \)

\(\displaystyle n = 2 \)　の場合は、\(\displaystyle \frac{1}{2} = 0.5 \times 12ヶ月 = 6ヶ月 \)なので半年の複利。半年ということは年に2回利子がつくので2乗する。

\(\displaystyle (1 + \frac{1}{2})^2 \)　→　\(\displaystyle (1 + 0.5)^2 = 2.25 \)

\(\displaystyle n = 4 \)　の場合は、\(\displaystyle \frac{1}{4} = 0.25 \times 12ヶ月 = 3ヶ月 \)なので3ヶ月の複利。3ヶ月ということは年に4回利子がつくので4乗する。

\(\displaystyle (1 + \frac{1}{4})^4 \)　→　\(\displaystyle (1 + 0.25)^4 = 2.44140625 \)

\(\displaystyle n = 12 \)　の場合は、\(\displaystyle \frac{1}{12} = 0.08333 \times 12ヶ月 = 1ヶ月 \)なので1ヶ月の複利。1ヶ月ということは年に12回利子がつくので12乗する。

\(\displaystyle (1 + \frac{1}{12})^{12} \)　→　\(\displaystyle (1 + 0.08333)^{12} = 2.61303 \)

\(\displaystyle n = 365 \)　の場合は、毎日利子がつくので365乗する。

\(\displaystyle n = 365 \)　→　\(\displaystyle (1 + \frac{1}{365})^365 \)　→　\(\displaystyle (1 + 0.00273937)^{365} = 2.714567\)

ネイピア数を求める式

連続複利の元利合計の例で挙げた\(\displaystyle n \)を限りなく大きくしていった場合の極限値がネイピア数(\(\displaystyle e \))ということになる。

\(\displaystyle e = \lim_{n \to \infty} (1 + \frac{1}{n})^n \)

また、年利が１でなくxの場合は、年利が1増加すると元利合計額はe倍ずつ増加していく。

\(\displaystyle e^x = \lim_{n \to \infty} (x + \frac{1}{n})^n \)

その他にも\(\displaystyle \sum\)と\(\displaystyle n \)の階乗を使って求めることができる。

\(\displaystyle e =  \sum_{n=0}^{\infty} \frac{1}{n!} \)

Pythonでネイピア数を求めてみる(1)

\(\displaystyle \lim_{n \to \infty} \)は、\(\displaystyle n \)から\(\displaystyle \infty \)(無限)まで、という意味。しかし、無限までの計算はできないので、今回は変化がわかりやすい100までで計算してみる。また、グラフを見て感覚的にネイピア数を理解する。

\(\displaystyle e = \lim_{n \to \infty} (1 + \frac{1}{n})^n \)

# グラフ描画ライブラリ
from matplotlib import pylab as plt

# 1から100までを計算し配列に格納していく
e = [(1 + (1 / n)) ** n for n in range(1, 100)]

# 配列の一番最後の数を出力する
print(e[-1])

# グラフをプロットする
plt.plot(e)
# y軸の100に赤線を引く
plt.hlines([math.e], 1, 100, "red", linestyles="dashed")

2.704679036164753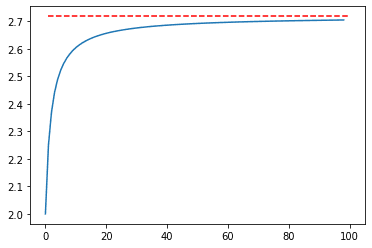

計算の回数(横軸)が増えていくに連れて変化が収束し、赤線のところに近づいていることがわかる。この赤線がネイピア数(2.718281828459045…)です。試しに計算回数を1000回にしてみる。

# グラフ描画ライブラリ
from matplotlib import pylab as plt

# 1から1000までを計算し配列に格納していく
e = [(1 + (1 / n)) ** n for n in range(1, 1000)]

# 配列の一番最後の数を出力する
print(e[-1])

# グラフをプロットする
plt.plot(e)
# y軸の100に赤線を引く
plt.hlines([math.e], 1, 100, "red", linestyles="dashed")

2.7169225742266474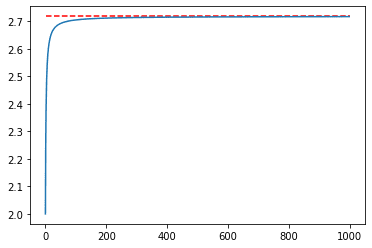

1000回ともなると赤線とほぼ同じになった。値もネイピア数(2.718281828459045…)に近づいている。また、ネイピア数は、無理数なので\(\displaystyle \pi \)のように数が永遠と続いていく。

Pythonでネイピア数を求めてみる(2)

下記の式もPyhonで実装してみる。

\(\displaystyle e =  \sum_{n=0}^{\infty} \frac{1}{n!} \)

import math
# 階乗する数
n = 1000
# ネイピア数
e = 0.0

for n in range(n):
    # n回階乗する
    e += 1 / math.factorial(n)

print(e)

実際は、このように計算しなくてもmathモジュールやnumpyにネイピア数が定義されている。

import math
import numpy as np

print(math.e)
print(np.e)