コサイン距離
コサイン距離は、2つのベクトルがどのくらい違う方向を向いているのかを表し、0から2の範囲の値をとる。0であれば「最も似ている」、2であれば「最も似ていない」、ということになる。ベクトルの長さは関係なく、なす角によって2つのベクトルの方向性の違いがわかる。
ベクトルx : \(\displaystyle x = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) \)
ベクトルy : \(\displaystyle y = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right) \)
コサイン距離 : \(\displaystyle d(x, y) = 1 – \cos\theta = 1 – \frac{x \cdot y}{||x||||y||}\)
Pythonでコサイン距離を求める
ユーザーA、B、C、Dの1週間の食事(7日×3食)で肉と魚どちらが多いのかアンケートを取り、肉と魚どちらの傾向が強いかをベクトル図で表してみる。
from matplotlib import pylab as plt
fig, ax = plt.subplots()
plt.xlabel('Meat')
plt.xlim([0, 20])
plt.ylabel('Fish')
plt.ylim([0, 20])
meal= {'A': [12, 4], 'B': [13, 3], 'C': [3, 12], 'D': [6, 12]}
for i, j in meal.items():
ax.annotate(i, xy=(j[0], j[1]))
ax.quiver(0, 0, j[0], j[1], angles='xy', scale_units='xy', scale=1)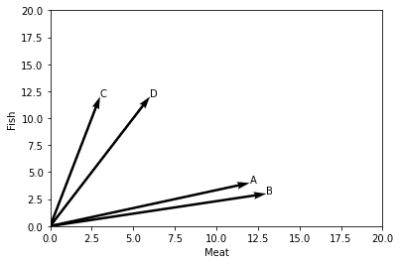
AとBは肉を食べる傾向にあり、CとDは魚を食べる傾向があるように見える。
次は、コサイン距離を求めてみる。
import numpy as np
import pandas as pd
def cosine(x, y):
# コサイン距離
d = 1 - x.dot(y) / (np.linalg.norm(x) * np.linalg.norm(y))
return d
meal = {'A': np.array([12, 4]), 'B': np.array([13, 3]), 'C': np.array([3, 12]), 'D': np.array([6, 12])}
idx = list()
distance_list = list()
for i in meal.keys():
for j in meal.keys():
idx.append('{} & {}'.format(i, j))
distance_list.append([cosine(meal[i], meal[j])])
pd.DataFrame(distance_list, index=idx, columns=['コサイン距離'])| コサイン距離 | |
|---|---|
| A & A | 2.220446e-16 |
| A & B | 4.504527e-03 |
| A & C | 4.631245e-01 |
| A & D | 2.928932e-01 |
| B & A | 4.504527e-03 |
| B & B | 0.000000e+00 |
| B & C | 5.455297e-01 |
| B & D | 3.631186e-01 |
| C & A | 4.631245e-01 |
| C & B | 5.455297e-01 |
| C & C | -2.220446e-16 |
| C & D | 2.381294e-02 |
| D & A | 2.928932e-01 |
| D & B | 3.631186e-01 |
| D & C | 2.381294e-02 |
| D & D | 1.110223e-16 |
コサイン距離では、BとCが一番離れておりグラフを見てもBとCが一番離れていると直感的にわかる。コサイン距離の値は0~2をとります。従って、上記では指数表示となっていますが全て0~2の範囲内です。
scipyでのコサイン距離
import scipy.spatial
meal= {'A': [12, 4], 'B': [13, 3], 'C': [3, 12], 'D': [6, 12]}
result = scipy.spatial.distance.cosine(meal['B'], meal['C'])
print(result)0.5455296583121261指数表示でなく小数点で表示されているが、BとCのコサイン距離と結果が同じになっている。
コサイン類似度
2つのデータを2本のn次元のベクトルとすると、コサイン距離が大きいということは、2つのベクトルは類似していないということであり、これは相関関係が小さいと言うことができる。
Pythonでコサイン類似度
まず、相関関係を求めてみる。データセットはKaggleから頂いた(2021-22 NBA Season Active NBA Players)を使ってみる。全NBA選手の身長と体重のデータセットです。Muhammet Ali Büyüknacarさん、度々ありがとうございます。
import scipy
from scipy.stats import pearsonr
from matplotlib import pylab as plt
# NBA選手
players = pd.read_csv('データセットのcsvのパス')
# グラフ描画
plt.scatter(players['Height_i'], players['Weight'])
# 身長と体重の相関関係
result = pearsonr(players['Height_i'], players['Weight'])[0]
print(result)0.3136257663596601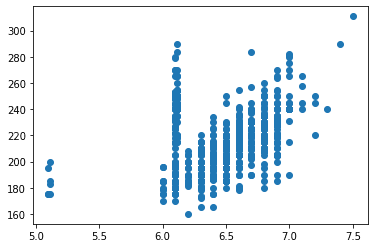
結果からは身長と体重の相関関係はそれほどなさそうです。
次にコサイン類似度を求めてみる。コサイン距離は0~2の範囲をとるので、1からコサイン距離を引くとコサイン距離の逆、つまりコサイン類似度を表すことになる。また、コサイン類似度を求める前に、全選手の身長、体重からそれぞれ平均値を差し引き、平均身長と平均体重を0にしておく。
import scipy
# NBA選手
players = pd.read_csv('/content/drive/MyDrive/nba_players.csv')
# 全選手の身長と体重から平均値を差し引く
players['Height_i'] = players['Height_i'] - np.mean(players['Height_i'])
players['Weight'] = players['Weight'] - np.mean(players['Weight'])
# コサイン距離
d = scipy.spatial.distance.cosine(players['Height_i'], players['Weight'])
print(d)
# コサイン類似度
s = 1 - scipy.spatial.distance.cosine(players['Height_i'], players['Weight'])
print(s)コサイン距離:0.6863742336403398
コサイン類似度:0.3136257663596602相関関係と同じ値が出力された。

記事を読んでいただきありがとうございました。