コインを投げたときに表が出るのか、それとも裏が出るのか、といったように試行した際に起こる結果が2つしかない試行のことをベルヌーイ試行といい、ある交差点で1年間に事故が起こる確率を考えてみると、事故が起こるか起こらないかのと考えることができるのでベルヌーイ試行と言うことができる。ただ、交差点で自己はそんなに多くなく年に1、2回あるかないか。このような低い確率で起こる事象を分析する際にポアソン分布が利用される。
\(\displaystyle Pr(k) \)は事象が\(\displaystyle k \)回起こる確率、\(\displaystyle \lambda \)は事象が平均で何回起こり得るか、\(\displaystyle e \)はネイピア数を表す。
ポアソン分布 : \(\displaystyle Pr(k) = \frac{\lambda^{k} e^{- \lambda}}{k!} \)
Pythonでポアソン分布を求める
from matplotlib import pylab as plt
from scipy.stats import poisson
data = list()
# 起こる平均を1~4の範囲で設定
for avg in range(1, 5):
data.append([poisson.pmf(k, avg) for k in range(0, 10)])
plt.plot(data[0], 'r', data[1], 'b', data[2], 'g', data[3], 'p', linestyle="dashdot")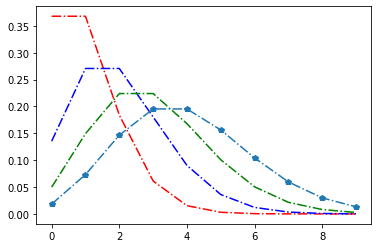
縦軸が確率、横軸が試行回数。赤線は事象が起こる平均が1回の場合、青が2回、緑が3回、紺色が4回。事象が平均1回しか起こらない場合は、試行回数が増えるにつれて確率が0%に近づいていき、他の8回目くらいから確率が0%に近づいて行っていることがわかる。
次に、1月~12月の事故の回数から事故が起こる確率をポアソン分布で求めてみる。
import math
import pandas as pd
def poisson_distribution(k, avg):
"""
ポアソン分布
param k : k
return : ポアソン分布
"""
result = (avg ** k) * (math.e ** -avg) / math.factorial(k)
return result
# 1月から12月までの事故の数
accidents = [0, 1, 2, 0, 3, 1, 0, 2, 1, 0, 2, 2]
# 事故が起こる平均
avg = sum(accidents) / len(accidents)
data = list()
# 0〜6まで結果を表示
for k in range(7):
data.append([poisson_distribution(k, avg) * 100])
pd.DataFrame(data, columns=['確率'])| 確率 | |
|---|---|
| 0 | 31.140322 |
| 1 | 36.330376 |
| 2 | 21.192719 |
| 3 | 8.241613 |
| 4 | 2.403804 |
| 5 | 0.560888 |
| 6 | 0.109061 |
月に1、2回起こる確率は高いが、月に5回、6回起こる確率はかなり低いことがわかる。

記事を読んでいただきありがとうございました。