>開発>python>[Pythonで統計]対数正規分布

[Pythonで統計]対数正規分布

対数正規分布

対数正規分布は、正規分布のように左右対称の山のような分布になるのではなく、右に向かって変化していく分布のこと。

正規分布
対数正規分布

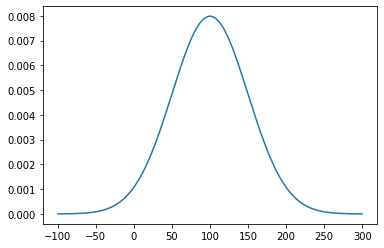
\(\displaystyle ln \)はネイピア数を底とする対数(自然対数)、\(\displaystyle m \)は相加平均、\(\displaystyle v \)は分散、\(\displaystyle erf \)は誤差関数を表す。

対数平均　:　\(\displaystyle \mu = ln \left(\frac{m}{\sqrt{1 + \frac{v}{m^2}}} \right) \)

対数標準偏差　:　\(\displaystyle \sigma^2 = ln \left( 1 + \frac{v}{m^2} \right) \)

確率密度関数　:　\(\displaystyle f(x) = \frac{1}{\sqrt{2 \pi}\sigma x} e^{- \frac{(ln x – \mu)^2}{2 \sigma^2}} \)

\(\displaystyle erfc(x) = 1 – erf(x) \)

累積分布関数　:　\(\displaystyle \frac{1}{2} erfc \left( \frac{ln x – \mu}{\sqrt2 \sigma} \right) \)

Pythonで対数正規分布を求める

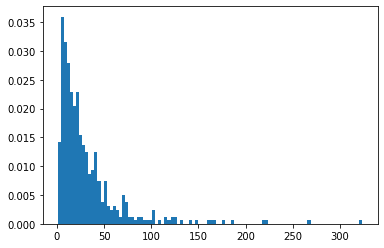
NBA選手の身長で185cmから230cmの選手の対数正規分布を求めてみる。データセットはKaggleでMuhammet Ali Büyüknacarさんの”2021-22 NBA Season Active NBA Players“を利用させていただく。

import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def log_normal_distribution(i, mu, sigma):
  # 対数正規分布
  x = (1 / (np.sqrt(2 * np.pi) * s * i))
  y = (np.e ** (- ((math.log(i) - mu) ** 2) / (2 * s ** 2)))
  result = x * y

  return result

# NBA選手のデータ
players = pd.read_csv('データセットのcsvのパス')
# フィートからセンチへ
heights = players['Height_i'] / 0.032808
# ポンドからキログラムへ
weights = players['Weight'] / 2.2046

# 身長の平均値
m = np.mean(heights)
# 身長の分散
v = np.var(heights)
# 対数平均
mu = np.log(m / np.sqrt(1 + v / (m ** 2)))        
# 対数標準偏差
std = np.log(1 + np.var(heights) / (np.mean(heights) ** 2))
sigma = np.sqrt(std)

# 185cmから230cmを1で刻む
range_list = np.arange(185, 230, 1)

# 対数正規分布を実行
n = [log_normal_distribution(i, mu, sigma) for i in range_list]
plt.plot(range_list, n)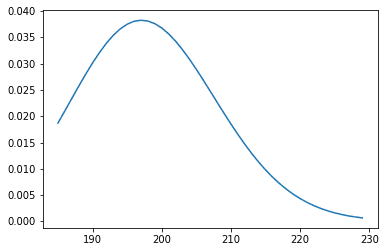

対数なので200cmの選手が際立って多いことが直感的にわかる。

scipyでの対数正規分布

scipyではlognorm関数で対数正規分布を実装できる。ここで注意すべきは、対数正規分布の求め方。ネイピア数を底とする対数(自然対数)を事前にとってから相加平均と標準偏差を求めているため、先程の関数と違う結果になる。

対数平均　:　\(\displaystyle \mu = \frac{1}{n} \sum_{i = 1}^{n} ln x_i \)

対数標準偏差　:　\(\displaystyle \sigma^2 = \frac{1}{n} \sum_{i = 1}^{n} (ln x_i – \mu)^2 \)

先程と同じく、NBA選手のデータセットから対数正規分布を求める。

import math
import numpy as np
import pandas as pd
from scipy.stats import lognorm

def log_normal_distribution(i, mu, sigma):
  # 対数正規分布
  x = (1 / (np.sqrt(2 * np.pi) * s * i))
  y = (np.e ** (- ((math.log(i) - mu) ** 2) / (2 * s ** 2)))
  result = x * y

  return result

# NBA選手のデータ
players = pd.read_csv('データセットのcsvのパス')
# フィートからセンチへ
heights = players['Height_i'] / 0.032808

# 身長の平均値
m = np.mean(heights)
# 身長の分散
v = np.var(heights)
# 対数平均
mu = np.log(m / np.sqrt(1 + v / (m ** 2)))        
# 対数標準偏差
std = np.log(1 + np.var(heights) / (np.mean(heights) ** 2))
sigma = np.sqrt(std)

# 対数正規分布(scipy)
s, loc, scale = lognorm.fit(heights, floc=0)
result1 = lognorm.pdf(190, s, loc=loc, scale=scale)
# 対数正規分布(独自)
result2 = log_normal_distribution(190, mu, sigma)

print(result1)
print(result2)
0.03015025438198185
0.030454822430871522

微小な差異ではあるがscipyと独自関数の出力結果が一致しないことがわかる。

数学

記事を読んでいただきありがとうございました。

Page Top