最小二乗法
最小二乗法は、気温が高いとビールの購買数が高くなり、気温が低くなると購買数が減るなど、データを分析し将来の顧客行動を予測するなど、一定の条件下で将来のデータを予測する際に用いられる。このように、相関関係のあるデータから特定の条件の値を予測することを回帰といい、求めたい値を目的変数、予測する元となる値を説明変数という。
二乗和誤差 : \( \displaystyle MSE = |sum_{i = 1}^{n} (y_i – f(x_i))^2 \)
\( \displaystyle {Cov_{x, y}} \)は、xとyの共分散、\(\displaystyle \sigma \)は分散を表す。
回帰直線 : \(\displaystyle f(x) = ax + b \)、\(\displaystyle a = \frac{Cov_{x, y}}{\sigma_x^2} \)、\(\displaystyle b = (\bar{y} – a\bar{x}) \)
Pythonで回帰直線を求める
説明変数\(\displaystyle (x) \)を身長とし、体重を目的変数\(\displaystyle (y) \)として予測するモデルを一次関数で表すと次のようになる。\(\displaystyle a \)は傾き、\(\displaystyle b \)は切片となる。傾きと切片が決まれば直線が決まるため、もっともそれらしい直線を決めていく。
\(\displaystyle f(x) = ax + b \)
NBA選手の身長で185cmから230cmの選手の対数正規分布を求めてみる。データセットはKaggleでMuhammet Ali Büyüknacarさんの”2021-22 NBA Season Active NBA Players“を利用させていただく。
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# NBA選手のデータ
players = pd.read_csv('データセットのcsvのパス')
# フィートからセンチへ
heights = players['Height_i'] / 0.032808
# ポンドからキログラムへ
weights = players['Weight'] / 2.2046
# 散布図(縦軸:体重、横軸:身長)
plt.scatter(heights, weights, s=25)
plt.xlim(160, 240)
plt.ylim(40, 180)
# 16ocmから240cmの範囲
x = np.arange(160, 240)
# モデル1
a1 = 1.0
b1 = 100
model1 = a1 * x - b1
plt.plot(x, model1, color='r')
# モデル2
a2 = 1.5
b2 = 180
model2 = a2 * x - b2
plt.plot(x, model2, color='g')
# モデル3
a3 = 2.0
b3 = 260
model3 = a3 * x - b3
plt.plot(x, model3, color='b')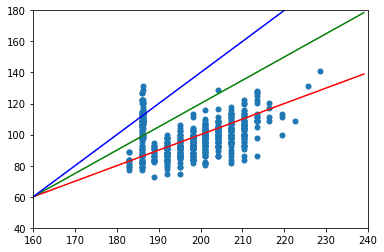
直感的に赤の線がもっともそれらしい直線だとわかる。
次は、直感的ではなく数値で評価してみる。
import copy
import pandas as pd
def rss(data):
"""
二乗和誤差
param data : データ
return : 二乗和誤差
"""
result = 0
for i in data.iterrows():
result += (i[1]['weight'] - i[1]['prediction']) ** 2
return result
# NBA選手のデータ
players = pd.read_csv('/content/drive/MyDrive/nba_players.csv')
# フィートからセンチへ
heights = players['Height_i'] / 0.032808
# ポンドからキログラムへ
weights = players['Weight'] / 2.2046
df = pd.DataFrame({'height':heights, 'weight':weights})
# モデル1
a1 = 1.0
b1 = 100
rss_model1 = copy.deepcopy(df)
rss_model1['prediction'] = a1 * rss_model1['height'] - b1
# モデル2
a2 = 1.5
b2 = 180
rss_model2 = copy.deepcopy(df)
rss_model2['prediction'] = a2 * rss_model2['height'] - b2
# モデル3
a3 = 2.0
b3 = 260
rss_model3 = copy.deepcopy(df)
rss_model3['prediction'] = a3 * rss_model3['height'] - b3
# 指数表示無効化
pd.options.display.float_format = '{:.2f}'.format
result = pd.DataFrame([[rss(rss_model1)], [rss(rss_model2)], [rss(rss_model3)]], index=['モデル1', 'モデル2', 'モデル3'], columns=['RSS'])| 二乗和誤差 | |
|---|---|
| モデル1 | 87533.00 |
| モデル2 | 336902.46 |
| モデル3 | 1015713.48 |
二乗和誤差は、値が低い方が精度が高いので、モデル1が最も精度が高く、モデル3が最も精度が低いことになる。グラフを見た時の直感と同じような結果が出た。
最小二乗法で求める
次は、最小二乗法で二乗和誤差が最も少ない直線を求める。
\(\displaystyle f(x) = ax + b \)
\(\displaystyle a = \frac{Cov_{x, y}}{\sigma_x^2} \)
\(\displaystyle b = (\bar{y} – a\bar{x}) \)
import copy
import pandas as pd
def cov(x, y):
"""
共分散
param x : 標本x
param y : 標本y
return : 共分散
"""
# 相加平均
x_mean = np.mean(x)
y_mean = np.mean(y)
# 要素数
n = len(x)
c = 0.0
for i in range(n):
x_i = x[i]
y_i = y[i]
c += (x_i - x_mean) * (y_i - y_mean)
# 共分散
cov = c / n
return cov
def std(x):
"""
標準偏差
param x : 標本
return : 標準偏差
"""
# 相加平均
mu = np.mean(x)
# 要素数
n = len(x)
std = 0.0
# 平均と要素の差を取って2乗する
for i in range(n):
std += (x[i] - mu) ** 2
std = std / n
sigma = np.sqrt(std)
return sigma
def slope(x, y):
"""
傾き
param x : 標本x
param y : 標本y
return : 傾きa
"""
a = cov(x, y) / (std(x) ** 2)
return a
def intercept(x, y):
"""
切片
param x : 標本x
param y : 標本y
return : 切片b
"""
# 相加平均
x_mean = np.array(x).mean()
y_mean = np.array(y).mean()
# 傾き
a = slope(x, y)
# 切片
b = y_mean - x_mean * a
return b
# NBA選手のデータ
players = pd.read_csv('/content/drive/MyDrive/nba_players.csv')
# フィートからセンチへ
heights = players['Height_i'] / 0.032808
# ポンドからキログラムへ
weights = players['Weight'] / 2.2046
df = pd.DataFrame({'height':heights, 'weight':weights})
# 傾きa
a = slope(df['height'], df['weight'])
# 切片b
b = intercept(df['height'], df['weight'])
# x軸の範囲
x = np.arange(160, 240)
# 予測された目的変数
y = a * x + b
# 回帰直線プロット
df.plot(kind='scatter', x='height', y='weight')
plt.xlim(160, 240)
plt.ylim(40, 180)
plt.plot(x, y, color='red')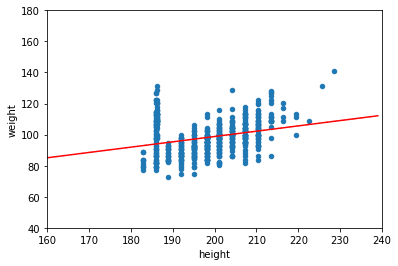
62398.249909167396先程のモデル1の直線とどちらがそれっぽい直線かは直感的にはわかりにくいが、二乗和誤差は”87533.00″から”62398.24″と減っているので精度が上がっている。

記事を読んでいただきありがとうございました。