バスタブ曲線
バスタブ曲線は、故障率曲線とも言い、電子機器などの故障率が時間経過とともにどうのように変化するかを表す。初期故障期、偶発的故障期、摩耗故障期に分けられ、初期故障期は不良品などの影響で比較的故障率が高く、初期故障期を過ぎると故障率は低くなり、しばらく経過すると部品の摩耗などで故障率が再び高くなる。これを、描くとバスタブのように曲線が描かれることからバスタブ曲線と呼ばれている。\(\displaystyle \lambda \)は、指数分布での曲線を描く際のパラメータで、\(\displaystyle \beta \)はどの期間でも一定確率故障が発生する故障率。\(\displaystyle t \)は経過時間、\(\displaystyle t_1 \)は初期故障期を、\(\displaystyle t_2 \)が摩耗故障期を表す。
バスタブ曲線 : \(\displaystyle \begin{eqnarray} f(t) = \left\{ \begin{array}{l} (\lambda e)^{- \lambda t} + \beta & t \lt t_1 \\ \beta & t_1 \leq t \lt t_2 \\ \alpha(t – t_2) & t_2 \leq t \end{array} \right. \end{eqnarray} \)
Pythonでバスタブ曲線を求める
まずは、1つ目の条件のような指数関数のバスタブ曲線をグラフにしてみる。故障率は0.1で、\(\displaystyle \lambda \)の値を0.1~2.0の範囲でグラフを描く。
バスタブ曲線 : \(\displaystyle f(t) = (\lambda e)^{- \lambda t} + \beta (t \lt t_1 ) \)
import math
import numpy as np
from matplotlib import pylab as plt
def bathtub_curve_1(t, lambd, beta):
# 指数分布
r = (lambd * math.e) ** (-lambd * t) + beta
return r
for lambd in list(range(1, 10)) + list(range(10, 30, 10)):
lambd /= 10
t = np.linspace(0, 10, 100)
plt.plot(t, bathtub_curve_1(t, lambd, 0.1), label='λ={0:.1f}'.format(lambd))
# グラフにlegendを表示
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)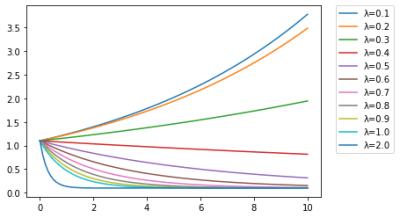
\(\displaystyle \lambda \)の値が大きくなるほど、バスタブ曲線らしくなっており、横軸(t:時間)が経過するにつれて故障率が下がっていることがわかる。
次に2つ目の条件は、ただの固定された\(\displaystyle \beta \)が出力されるだけ。3つ目の条件は、故障率が線形になることが想像できる。
バスタブ曲線 : \(\displaystyle f(t) = \alpha(t – t_2) (t_2 \leq t) \)
import numpy as np
from matplotlib import pylab as plt
def bathtub_curve_2(t, t2, alpha, beta):
result = alpha * (t - t2) + beta
return result
t = np.linspace(1, 10, 100)
plt.plot(t, bathtub_curve_2(t, 10, 0.5, 0.1))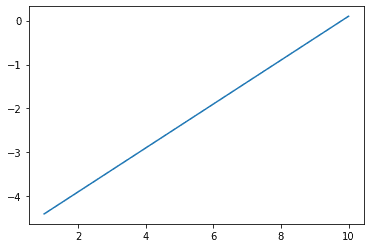
最後にすべての条件を出力してみる。
バスタブ曲線 : \(\displaystyle \begin{eqnarray} f(t) = \left\{ \begin{array}{l} (\lambda e)^{- \lambda t} + \beta & t \lt t_1 \\ \beta & t_1 \leq t \lt t_2 \\ \alpha(t – t_2) & t_2 \leq t \end{array} \right. \end{eqnarray} \)
import math
import numpy as np
from matplotlib import pylab as plt
def bathtub_curve_1(t, lambd, beta):
r1 = (lambd * math.e) ** (-lambd * t) + beta
return r1
def bathtub_curve_2(t, t2, alpha, beta):
r2 = alpha * (t - t2) + beta
return r2
def bathtub_curve(t, t2, lambd, alpha, beta):
if t < 2:
# 初期故障期
return bathtub_curve_1(t, lambd, beta)
elif t < t2:
# 偶発故障期
return beta
else:
# 摩耗故障期
return bathtub_curve_2(t, t2, alpha, beta)
t = np.linspace(0, 10, 100)
# 摩耗故障期の時期
t2 = 6
plt.plot(t, [bathtub_curve(i, t2, 1.5, 0.5, 0.1) for i in t])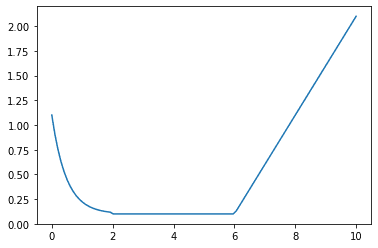
経過劣化した後の摩耗故障期の故障率は1次関数で直線となっているが、バスタブっぽくなっている。
また、バスタブ曲線を描くだけならガンマ関数でも可能です。
import numpy as np
from matplotlib import pylab as plt
from scipy import special
t = np.linspace(0, 5, 100)
plt.plot(t, special.gamma(t))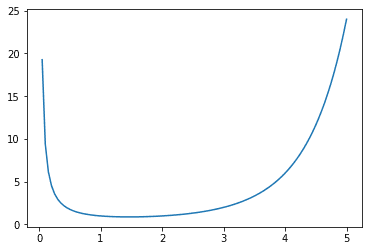

記事を読んでいただきありがとうございました。