目次
ベクトル
ベクトルは、大きさと向きを持つ量のこと。1個の数の場合は、1次元ベクトル、2個の場合は2次元ベクトル、3個の場合は3次元ベクトル、n個の場合はn次元ベクトルと言う。
縦ベクトル : \(\displaystyle \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) \)
\(\displaystyle T \)は、ベクトル\(\displaystyle x \)の転置行列を表している。転置行列は、行列の行と列を入れ替えた時の行列。縦ベクトルを転置行列で表すと横ベクトルになる。
横ベクトル : \(\displaystyle x^T = (x_1, x_2, \dots, x_n) \)
ベクトルの長さ : \(\displaystyle \vert \vert x \vert \vert = \sqrt{\sum_{k=1}^n} x_k^2 \)
Pythonでベクトルの足し算を求める
ベクトルは、リストで表現することができる。また、ベクトルはスカラーなので、普通に足し算、引き算ができる。まずは、ベクトルの足し算を考えてみる。
from matplotlib import pylab as plt
# ベクトルx
x = [1, 4]
# ベクトルy
y = [2, 3]
add_result = [0, 0]
for i in range(len(x)):
# ベクトルの足し算
add_result[i] = x[i] + y[i]
print(add_result)
fig, ax = plt.subplots()
# xとy軸の制限
plt.xlim([0, 10])
plt.ylim([0, 10])
# 注釈
ax.annotate('x', xy=(x[0], x[1]))
ax.annotate('y', xy=(y[0], y[1]))
ax.annotate('result', xy=(add_result[0], add_result[1]))
# ベクトル場
ax.quiver(0, 0, x[0], x[1], angles='xy', scale_units='xy', scale=1)
ax.quiver(0, 0, y[0], y[1], angles='xy', scale_units='xy', scale=1)
ax.quiver(0, 0, add_result[0], add_result[1], angles='xy', scale_units='xy', scale=1)[3, 7]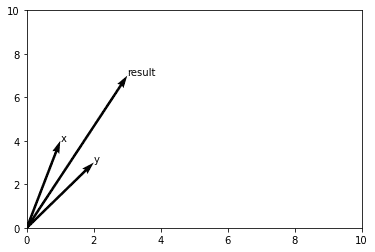
このように、ベクトルの足し算、引き算はリストのそれぞれの要素が足し算、引き算されて出力されるだけ。グラフでは、ベクトルの足し算した結果は、ベクトルxとベクトルyの隣り合う辺とする平行四辺形の対角線となる。
Pythonでベクトルの引き算を求める
次にベクトルの引き算を考えてみる。
from matplotlib import pylab as plt
# ベクトルx
x = [1, 6]
# ベクトルy
y = [4, 2]
sub_result = [0, 0]
for i in range(len(x)):
# ベクトルの引き算
sub_result[i] = x[i] - y[i]
print(sub_result)
fig, ax = plt.subplots()
# xとy軸の制限
plt.xlim([-10, 10])
plt.ylim([-10, 10])
# 注釈
ax.annotate('x', xy=(x[0], x[1]))
ax.annotate('y', xy=(y[0], y[1]))
ax.annotate('-y', xy=(-y[0] - 0.5, -y[1]))
ax.annotate('sub_result', xy=(sub_result[0] - 2, sub_result[1]))
# ベクトル場
ax.quiver(0, 0, x[0], x[1], angles='xy', scale_units='xy', scale=1)
ax.quiver(0, 0, y[0], y[1], angles='xy', scale_units='xy', scale=1)
ax.quiver(0, 0, -y[0], -y[1], angles='xy', scale_units='xy', scale=1)
ax.quiver(0, 0, sub_result[0], sub_result[1], angles='xy', scale_units='xy', scale=1)[-3, 4]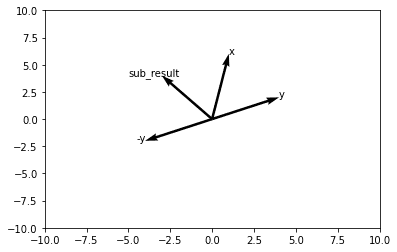
\(\displaystyle x – y = x + (-y) \)なので、ベクトルの引き算は、ベクトルyの反対向きのベクトル、つまりベクトル-yとベクトルxの隣り合う辺とする平行四辺形の対角線となる。
Pythonでベクトルの長さを求める
\(\displaystyle \vec{x} = \left( \begin{array}{c} 3 \\ 4 \end{array}\right) \)のベクトルの長さを求めてみる。
ベクトルの長さ : \(\displaystyle \vert \vert x \vert \vert = \sqrt{\sum_{k=1}^n} x_k^2 \)
計算すると次のようになる。\(\displaystyle \vert \vert x \vert \vert = \sqrt{\sum_{k=1}^2} x_k^2 = \sqrt{3^2 + 4^2} = 5 \)
import math
x = [3, 4]
long = 0
for i in x:
long += math.pow(i, 2)
result = math.sqrt(long)
print(result)5.0ちゃんと、結果が5.0となった。
numpyでのベクトル
numpyでもベクトルを扱うことができる。また、norm関数でベクトルの長さを求めることができる。
import numpy as np
x = np.array([3, 4])
y = np.array([2, 3])
# 足し算
print(x + y)
# 引き算
print(x - y)
# 長さ
long = np.linalg.norm(x)
print(long)[5 7]
[1 1]
5.0内積
内積は、ベクトルの掛け算に相当する。また、\(\displaystyle \theta \)は、2つのベクトルがなす角を表す。
ベクトルx : \(\displaystyle x = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) \)
ベクトルy : \(\displaystyle y = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right) \)
内積 : \(\displaystyle x \cdot y = \sum_{k=1}^{n} x_k y_k = \vert \vert x \vert \vert \vert \vert y \vert \vert \cos \theta \)
Pythonで内積を求める
# ベクトルx
x = [3, 2]
# ベクトルy
y = [4, 5]
inner_product = 0
for i in range(len(x)):
# 角ベクトルの要素を掛けるて足し合わせていく
inner_product += x[i] * y[i]
print(inner_product)22このように、\(\displaystyle x \cdot y = 3 \times 4 + 2 \times 5 = 22 \)となる。
numpyでの内積
numpyでは、numpyのdot関数で内積を実装できる。
import numpy as np
# ベクトルx
x = np.array([3, 2])
# ベクトルy
y = np.array([4, 5])
# 内積
inner_product = x.dot(y)
print(inner_product)22Pythonで内積の角度を求める
2つのベクトルの角度を内積から求める。
内積 : \(\displaystyle x \cdot y = \vert \vert x \vert \vert \vert \vert y \vert \vert \cos \theta \)
上記の式を変形すると角度\(\displaystyle \theta \)を求めることができる。
\(\displaystyle \cos \theta \ = \frac{x \cdot y}{\vert \vert x \vert \vert \vert \vert y \vert \vert} \)
\(\displaystyle \vert \vert x \vert \vert \vert \vert y \vert \vert \)は、それぞれベクトルxとベクトルyの長さのことで、numpyのnorm関数で求められる。
import numpy as np
# ベクトルx
x = np.array([3, 2])
# ベクトルy
y = np.array([4, 5])
# 角度
theta = x.dot(y) / (np.linalg.norm(x) * np.linalg.norm(y))
print(theta)0.9529257800132621
記事を読んでいただきありがとうございました。