>開発>python>[Pythonで数学]ユークリッド距離とマンハッタン距離

[Pythonで数学]ユークリッド距離とマンハッタン距離

ユークリッド距離

ユークリッド距離は、空間にある2つの距離を求めることができる。ピタゴラスの定理(三平方の定理)によって与えられる。\(\displaystyle d(x, y) \)は、座標\(\displaystyle (x, y) \)の距離\(\displaystyle d \)を求めるということ。

ベクトルx　:　\(\displaystyle x = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) \)

ベクトルy　:　\(\displaystyle y = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right) \)

ユークリッド距離　:　\(\displaystyle d(x, y) = \sqrt{(x_1 – y_1)^2 + (x_2 – y_2)^2 + \cdots + (x_n – y_n)^2} = \sqrt{\sum_{i = 1}^{n}(x_i – y_i)^2} \)

Pythonでユークリッド距離を求める

鳥取、大阪、東京の緯度・経度からユークリッド距離を求めてみる。因みに緯度は、\(\displaystyle 1^{ \circ } \)あたり約111kmで、経度は、(\displaystyle 1^{ \circ } \)あたり約91kmとなる。

import numpy as np
import pandas as pd

# 鳥取の緯度・経度
tottori = [35.30 * 111, 134.14 * 91]
# 大阪の緯度・経度
osaka = [34.41 * 111, 135.31 * 91]
# 東京の緯度・経度
tokyo = [35.41 * 111, 139.41 * 91]

def euclid(x, y):
  # 距離
  d = 0

  for i in range(len(x)):
      d += (x[i] - y[i]) ** 2
  
  result = np.sqrt(d)
  
  return result

d1 = euclid(tottori, osaka)
d2 = euclid(tottori, tokyo)

pd.DataFrame([d1, d2],index=['鳥取・大阪', '鳥取・東京'], columns=['ユーグリッド距離'])

ユーグリッド距離 鳥取・大阪間 145.242298 鳥取・東京間 479.725410

ユーグリッド距離
鳥取・大阪145.242298
鳥取・東京479.725410

Googleマップなどは道路の距離なので比較はできないが、直線に移動できればこれくらいの距離ということ。

numpyでのユークリッド距離

numpyのsum関数で総和とっていく方法もあるが、norm関数でベクトルの大きさを計算しても距離が求まる。

import numpy as np

# 鳥取の緯度・経度
tottori = [35.30 * 111, 134.14 * 91]
# 大阪の緯度・経度
osaka = [34.41 * 111, 135.31 * 91]

# numpy配列へ変換
tottori = np.array(tottori)
osaka = np.array(osaka)

# ユークリッド距離
result1 = np.sqrt(np.sum((tottori - osaka) ** 2))
result2 = np.linalg.norm(tottori - osaka)

print(result1)
print(result2)
145.2422975582548
145.2422975582548

scipyでのユークリッド距離

scipyではeuclidean関数でユークリッド距離を実装できる。

from scipy.spatial.distance import euclidean

# 鳥取の緯度・経度
tottori = [35.30 * 111, 134.14 * 91]
# 大阪の緯度・経度
osaka = [34.41 * 111, 135.31 * 91]

# ユークリッド距離
result = euclidean(tottori, osaka)

print(result )
145.2422975582548

標準化ユークリッド距離

標準化ユークリッド距離は、通常のユークリッド距離と違い、各要素の差を標準偏差で割る。1つの次元が他の次元と比べ極めて大きな値をとる場合、その次元の影響により全体の距離の大小が決まってしまうことがあるため、各次元のスケールをある程度、同じスケールで比べられるようにする。

標準化ユークリッド距離　:　\(\displaystyle d(x, y) = \sqrt{\sum_{i = 1}^{n}(\frac{x_i – y_i}{\sigma_i})^2} \)

Pythonで標準化ユークリッド距離を求める

通常のユークリッド距離同様に、緯度・経度で考える。

import numpy as np
import pandas as pd

# 鳥取の緯度・経度
tottori = [35.30 * 111, 134.14 * 91]
# 大阪の緯度・経度
osaka = [34.41 * 111, 135.31 * 91]
# 東京の緯度・経度
tokyo = [35.41 * 111, 139.41 * 91]

# 標準偏差
std_x = np.std([tottori[0], osaka[0], tokyo[0]])
std_y = np.std([tottori[1], osaka[1], tokyo[1]])
std = [std_x, std_y]

def std_euclidean(x, y, std):
    # 距離
    d = 0

    for i in range(len(x)):
        d += ((x[i] - y[i]) / std[i]) ** 2
    result = np.sqrt(d)
    
    return result 

pd.DataFrame([[std_euclidean(tottori, osaka, std)], [std_euclidean(tottori, tokyo, std)]], index=['鳥取・大阪', '鳥取・東京'], columns=['標準化ユーグリッド距離'])
標準化ユーグリッド距離
鳥取・大阪2.054115
鳥取・東京2.345184

scipyでの標準化ユークリッド距離

scipyの場合は、seuclidean関数で標準化ユークリッド距離を実装できる。ただし、引数は、標準偏差でなく分散を渡す必要があるため、numpyのvar関数で分散を計算する。

import numpy as np
from scipy.spatial.distance import seuclidean

# 鳥取の緯度・経度
tottori = [35.30 * 111, 134.14 * 91]
# 大阪の緯度・経度
osaka = [34.41 * 111, 135.31 * 91]
# 東京の緯度・経度
tokyo = [35.41 * 111, 139.41 * 91]

# 標準化ユークリッド
result1 = seuclidean(tottori, osaka, [np.var([tottori[0], tokyo[0], osaka[0]]), np.var([tottori[1], tokyo[1], osaka[1]])])
result2 = seuclidean(tottori, tokyo, [np.var([tottori[0], tokyo[0], osaka[0]]), np.var([tottori[1], tokyo[1], osaka[1]])])

print(result1)
print(result2)
2.0541152690478395
2.3451838098753446

同じ結果となった。

マンハッタン距離

ユークリッド距離がピタゴラスの定理(三平方の定理)のように直線的に距離を求めるなら、マンハッタン距離はx軸に進んで、y軸に進んで、といったように距離を求めるようなイメージ。

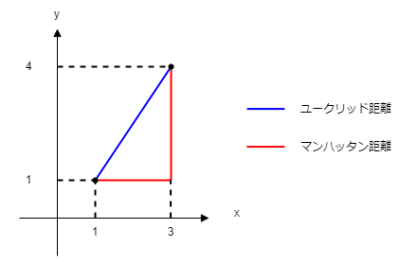
マンハッタン距離　:　\(\displaystyle d(x, y) = \sum_{i = 1}^{n} |x_i -y_i| \)

Pythonでマンハッタン距離を求める

ユークリッド距離で使った、緯度・経度をそのまま使ってマンハッタン距離を求めてみる。

import numpy as np
from scipy.spatial.distance import seuclidean

# 鳥取の緯度・経度
tottori = [35.30 * 111, 134.14 * 91]
# 大阪の緯度・経度
osaka = [34.41 * 111, 135.31 * 91]
# 東京の緯度・経度
tokyo = [35.41 * 111, 139.41 * 91]

def manhattan(x, y):
  # 距離
  d = 0

  for i in range(len(x)):
    d += np.abs(x[i] - y[i])

  return d

pd.DataFrame([[manhattan(tottori, osaka)], [manhattan(tottori, tokyo)]], index=['鳥取・大阪', '鳥取・東京'], columns=['マンハッタン距離'])
マンハッタン距離
鳥取・大阪205.26
鳥取・東京491.78

ユークリッド距離で求めた結果よい長くなっているが、目的地まで道路が一直線でないので、こちらの方が実際に運転する距離に近い。

数学

記事を読んでいただきありがとうございました。

Page Top