積分
積分は、簡単にまとめると直線や曲線で囲まれた範囲の面積を求めること。
積分 : \(\displaystyle \int_a^b f(x)dx \)
リーマン積分は、領域を細かく長方形に分け、その面積を合算して計算する。
リーマン積分 : \(\displaystyle \int_a^b f(x)dx = \lim_{n \to \infty } \sum_{k=1}^{n} \frac{b – a}{n} f (a + k) \cdot \frac{b – a}{n} \)
Pythonで積分を求める
まずは三角形の面積を考えてみる。三角形の面積は、\(\displaystyle \frac{底辺 \times 高さ}{2} \)なので、\(\displaystyle f(x) = 2x \)の場合は、下記のように求めることができる。
import numpy as np
from matplotlib import pylab as plt
def f(x):
y = 2 * x
return y
area = 10 * f(10) /2
print(area)
p = np.linspace(0, 10, 100)
plt.plot(p, f(p), color='r')
plt.fill_between(p, np.zeros(100), f(p), facecolor='r', alpha=0.1)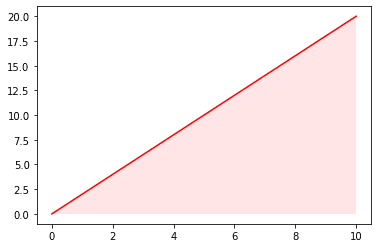
次は二次関数\(\displaystyle f(x) = x^2 \)で考えてみる。
import numpy as np
from matplotlib import pylab as plt
def f(x):
y = x ** 2
return y
p = np.linspace(0, 5, 100)
plt.plot(p, f(p), color='g')
plt.fill_between(p, np.zeros(100), f(p), facecolor='g', alpha=0.1)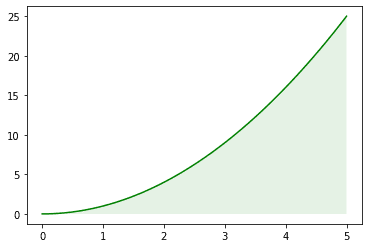
曲線が出てくるため簡単に面積を求めることができない。そこで、積分を使って求める。
import numpy as np
from matplotlib import pylab as plt
def f(x):
# 2次関数
y = x ** 2
return y
def integral(a, b, n):
# リーマン積分
d = (b - a) / n
s = 0
for i in range(n):
s += d * f(a + (i + 1) * d)
return s
result = integral(0, 5, 1000)
print(result)41.72918749999999\displaystyle n \)の数だけ領域を長方形で分けることになるので、\displaystyle n \)の値を大きくすればするほど精度の高い結果が得られる。
また、積分はscipyのintegral.quad関数で実装できる。
import numpy as np
import pandas as pd
from scipy import integrate
def f(x):
# 2次関数
y = x ** 2
return y
result, err = integrate.quad(f, 0, 5)
print(result)41.66666666666666誤差はあるものの近い値が出力された。また、printしていないが変数errには推定誤差が出力されている。
積分はたくさん演算を行うため、処理が重たい。実際に、先程作った積分の関数とspicyの関数で計測してみる。計測するには、”%time”をつけて関数を実行するだけ。
%time r = integral(0, 5, 100000)
%time r = integrate.quad(f, 0, 5)CPU times: user 27.7 ms, sys: 0 ns, total: 27.7 ms
Wall time: 27.7 ms
CPU times: user 41 µs, sys: 0 ns, total: 41 µs
Wall time: 44.1 µs作った関数の方は単位が”ms”でspicyの関数の方は”µs”となっていることから、spicyの関数の方がより早く、精度の高い結果を得ることができる。

記事を読んでいただきありがとうございました。