カイ二乗分布
カイ二乗分布は確率分布の一種で、推計統計学でよく利用されており、自由度 である\(\displaystyle k \)の\(\displaystyle X^2 \)が従う確率分布。自由度\(\displaystyle k \)は起こり得る結果から1を引いた数になる。例えば、コインを投げると結果は表か裏かの2つになるので\(\displaystyle 2 – 1 = 1 \)となる。
サイコロは\(\displaystyle \frac{1}{6} \)の確率で6の目が出るが、仮に100回試行し、60回も6の目が出たら明らかに多すぎるのでイカサマだと考えてしまう。このように明らかにおかしいといったことを直感的にわかるのがカイ二乗分布。
大文字のガンマ\(\displaystyle \Gamma \)はガンマ関数、小文字のガンマ\(\displaystyle \gamma \)は不完全ガンマ関数、\(\displaystyle E_i \)は期待値を表す。
確率密度関数 : \(\displaystyle f(x; k) = \frac{(\frac{1}{2})^{\frac{k}{2}}}{\Gamma (\frac{k}{2})} x^{\frac{k}{2} – 1} e^{\frac{-x}{2}} \)
ガンマ関数(1) : \(\displaystyle \gamma(n) = (n – 1)! \)
ガンマ関数(2) : \(\displaystyle \gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt( \Re_z > 0) \)
カイ二乗分布 : \(\displaystyle X^2 = \sum_{i = 1}^{k} \left( \frac{x_i -E_i}{E_i} \right)^2 \)
Pythonでカイ二乗分布を求める
まず、カイ二乗分布の関数を作成し、自由度を1から5の範囲でどのようなグラフを描くか見てみる。
確率密度関数 : \(\displaystyle f(x; k) = \frac{(\frac{1}{2})^{\frac{k}{2}}}{\Gamma (\frac{k}{2})} x^{\frac{k}{2} – 1} e^{\frac{-x}{2}} \)
import math
import numpy as np
from scipy.special import gamma
def chi_square_distribution(x, k):
"""
確率密度関数によるカイ二乗分布
param x : x
param k : 自由度
return : カイ二乗分布
"""
p = ((1 / 2) ** (k / 2)) / gamma(k / 2)
q = x ** ((k / 2) - 1) * (math.e ** (-x / 2))
result = p * q
return result
# 微小なt
t = np.linspace(0.001, 10, 100)
# 自由度1~5の範囲
for k in range(1, 6):
y = [chi_square_distribution(x, k) for x in t]
plt.plot(t, y, label='k=%d' % k)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.ylim([0.0, 1.0])
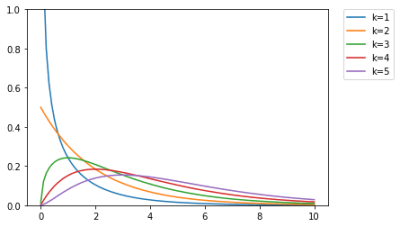
縦軸が確立密度で横軸がカイ二乗の値。カイ二乗分布は期待値との差を2乗した値を分布しているため、どれくらいまでなら現実的な事象のと言えるのかが直感的にわかる。
次にサイコロでカイ二乗分布を求めてみる。サイコロの目は6個なので自由度は\(\displaystyle 6 – 1 = 5 \)となる。
import math
import numpy as np
from scipy.special import gamma
def chi_square_distribution(x, k):
"""
確率密度関数によるカイ二乗分布
param x : x
param k : 自由度
return : カイ二乗分布
"""
p = ((1 / 2) ** (k / 2)) / gamma(k / 2)
q = x ** ((k / 2) - 1) * (math.e ** (-x / 2))
result = p * q
return result
# 微小なt(試行回数100回)
t = np.linspace(0.001, 100, 100)
# 自由度
k = 5
# カイ二乗分布
y = [chi_square_distribution(x, k) for x in t]
plt.plot(t, y)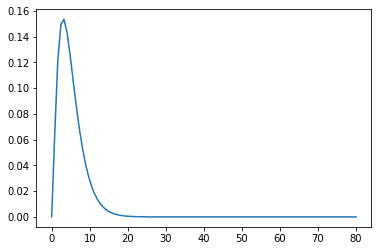
グラフを見てみると20あたりから確率密度がほぼ0になっている。つまり、100回サイコロを転がしても同じ目が20回出ることはほぼありえないということがわかる。
次は期待値からカイ二乗を求める。サイコロを100回転がして1の目が出る期待値は\(\displaystyle \frac{1}{6} \times 100 = \frac{100}{6} = \frac{50}{3} \)となる。
def chi_square_distribution(e, x):
"""
カイ二乗
param e : 期待値
param x : x
return : カイ二乗
"""
result = 0
for i in x:
result += ((i - e) ** 2) / e
return result
# 期待値
e = 50 / 3
# サイコロの目が出た回数(1の目が40回)
dice = [40, 20, 10, 10, 10, 10]
print(chi_square_distribution(e, dice))43.999という結果が出た。先程のグラフからもわかるように、1の目が40回も出るのはほぼありえないということがわかる。
scipyでのカイ二乗
scipyではchisquare関数でカイ二乗を実装することができる。
from scipy import stats
# 期待値
e = 50 / 3
# サイコロの目が出た回数(1の目が40回)
dice = [40, 20, 10, 10, 10, 10]
print(stats.chisquare(dice, f_exp=e))Power_divergenceResult(statistic=43.99999999999998, pvalue=2.316223940754832e-08)statisticがカイ二乗の値で、先程と同じ結果が出力されている。pvalueはp値のことで、事象が偶然発生する確率のこと。一般的には、\(\displaystyle p < 0.05 \)のときは、起こり得ないと判断する。
累積分布関数でp値求めることができ、scipyのgammainc関数で実装できる。
累積分布関数 : \(\displaystyle F(x; k) = \frac{\gamma(\frac{k}{2}, \frac{x}{2})}{\Gamma(\frac{k}{2})} \)
from scipy.special import gammainc
def chi_square_distribution(e, x):
"""
カイ二乗
param e : 期待値
param x : x
return : カイ二乗
"""
result = 0
for i in x:
result += ((i - e) ** 2) / e
return result
# 期待値
e = 50 / 3
# サイコロの目が出た回数(1の目が40回)
dice = [40, 20, 10, 10, 10, 10]
result = 1 - gammainc(5 / 2, chi_square_distribution(e, dice) / 2)
print(result)2.3162239459750822e-08scipyのchisquare関数と同じp値が出力された。

記事を読んでいただきありがとうございました。