ベータ分布

ベータ分布は、ベータ関数を利用して分布する。連続確率分布の一種で、ある試行で成功数を\(\displaystyle \alpha \)、失敗数を\(\displaystyle \beta \)とした時の成功率を\(\displaystyle p \)の分布を表す。例えばコインを100回投げて表(成功)\(\displaystyle \alpha \)60回、裏(失敗)\(\displaystyle \beta \)を40回とすると

\(\displaystyle \beta(a, b) \)はベータ関数を表す。また、\(\displaystyle p \)は確率で0から1の範囲をとる。

ベータ分布確率密度関数　:　\(\displaystyle f(p, a, b) = \frac{p^{a -1}(1 -p)^{b – 1}}{\beta(a, b)}, 0 < p < 1 \)

ベータ関数　:　\(\displaystyle \beta(x, y) = \int_0^1 t^{x-1} (t – t)^{y-1} dt ( \Re_x > 0, \Re_y > 0) \)

ベータ分布における平均　:　\(\displaystyle \frac{a}{a + b} \)

ベータ分布における最頻値　:　\(\displaystyle \frac{a – 1}{a + b – 2}, a,b > 1 \)

ベータ関数はガンマ関数を使って表すことができるので、ベータ分布もガンマ関数で表すことができる。

ガンマ関数とベータ関数　:　\(\displaystyle B(x, y) = \frac{\gamma (x) \gamma (y)}{\gamma (x + y)} \)

ベータ分布確率密度関数　:　\(\displaystyle f(p, a, b) = \frac{\gamma(a + b)}{\gamma(a)\gamma(b)}x^{a – 1}(1 – x)^{b -1} \)

Pythonでベータ分布を求める

何はともあれ、まずはベータ分布を実装してみる。

ベータ分布確率密度関数　:　\(\displaystyle f(p, a, b) = \frac{\gamma(a + b)}{\gamma(a)\gamma(b)}x^{a – 1}(1 – x)^{b -1} \)

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

# 成功数aと失敗数b
data = [(1, 1), (0.3, 0.3), (3, 1), (1, 3), (3, 3)]

for a, b in data:
  # ベータ関数
  bata_result = beta(a, b)
  # 0から1を100等分
  t = np.linspace(0, 1, 100)
  plt.plot(t, bata_result.pdf(t), label='a={0}, b={1}'.format(a, b))

plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)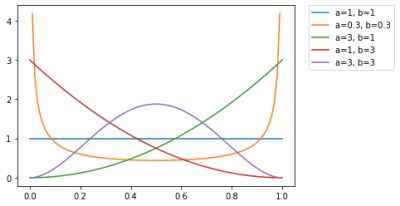

上記のように成功数aと失敗数bで形状が大きく変わる。

1. \(\displaystyle \alpha = \beta = 1 \) の場合は、一様分布になり、平均値 = 最頻値となる。
2. \(\displaystyle \alpha = \beta > 1 \) の場合は、正規分布のようになり、これも平均値 = 最頻値となる。
3. \(\displaystyle \alpha > \beta \) の場合は、左肩下がりのグラフになり、最頻値が平均値より右側になる。
4. \(\displaystyle \alpha < \beta \) の場合は、右肩下がりのグラフになり、平均値が最頻値より右側になる。

次に20%の確率で当たりを引くことができるくじ引きのベータ分布を見てみる。成功数\(\displaystyle \alpha \)と失敗数\(\displaystyle \beta \)は\(\displaystyle \frac{3}{15} = \frac{7}{35} = \frac{20}{100} \)、とどれも20%になっている。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

# 確率が20%になる成功数aと失敗数b
data = [(3, 12), (7, 28), (20, 80)]

for a, b in data:
  bata_result  = beta(a, b)
  t = np.linspace(0, 1, 100)
  plt.plot(t, bata_result .pdf(t), label='a={0}, b={1}'.format(a, b))

plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)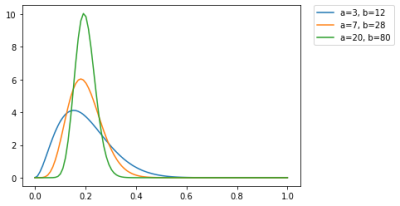

同じ20%といってもa=3、b=12の時のグラフの方は0%から40%の範囲の確率で起こりえそうだが、a=20、b=80の場合のグラフでは10%から30%くらいで収束し、ほぼほぼ20%の確率で起こり得えそうな感じだ。

当たる確率20%とする事前確率と実際に試行した後の確率とする事後確率を踏まえて計算してみる。まず、事前確率として100本引いて20本の当たりが出たとする(確率20%)。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import beta

def beta_distribution(p, a, b):
  """
  ベータ分布
  param p: 確率
  param a: 成功数
  param b: 失敗数
  return: ベータ分布
  """
  result = (p ** (a - 1) * ((1 - p) ** (b - 1))) / beta(a, b)
  return result

# 成功数
a = 20 
# 失敗数
b = 80

# 微小なt
t = np.linspace(0, 1, 100)
y = [beta_distribution(p, a, b) for p in t]

plt.plot(t, y)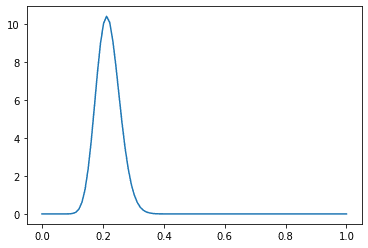

次に事後確率として、ユーザーAが10本引いて5本当たりを引いたとする(確率50%)。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import beta

def beta_distribution(p, a, b):
  """
  ベータ分布
  param p: 確率
  param a: 成功数
  param b: 失敗数
  return: ベータ分布
  """
  result = (p ** (a - 1) * ((1 - p) ** (b - 1))) / beta(a, b)
  return result

# 成功数
a = 20 + 5
# 失敗数
b = 80 + 5
# ベータ分布における最頻値
r = (a - 1) / (a + b - 2)
print(r)

# 微小なt
t = np.linspace(0, 1, 100)

y = [beta_distribution(p, a, b) for p in t]

plt.plot(t, y)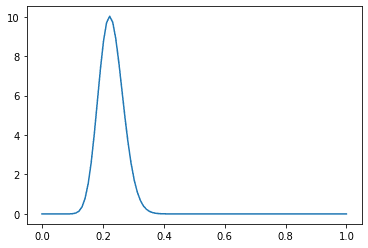

0.2222222222222222

最頻値は、22.2%となっており、ユーザーAが10本中5本と50%の確率で当たりを引いたからといって確率はそこまで変化しないことがわかる。これは、すでに100回とある程度、試行回数が多いからだ。このように最初に設定した確率、事前確率から補正した結果、事後確率を導いていくような方法をベイズ推定という。

scipyでのベータ分布

scipyでは、beta_dist関数でベータ分布を実装することができる。先程と同じ条件で計算してみる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta as beta_dist

# 成功数
a = 20
# 失敗数
b = 80
# 微小なt
t = np.linspace(0, 1, 100)
# ベータ分布
r = beta_dist(a, b)
plt.plot(t, r.pdf(t), color='g', alpha=0.5)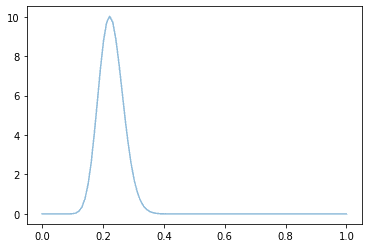

同じグラフが出力された。

ガンマ関数によるベータ分布

ベータ関数はガンマ関数で表すことができるため、ガンマ関数からベータ分布を導くことができる。

ガンマ関数(1)　:　\(\displaystyle \gamma(n) = (n – 1)! \)

ガンマ関数(2)　:　\(\displaystyle \gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt( \Re_z > 0) \)

ガンマ関数とベータ関数　:　\(\displaystyle B(x, y) = \frac{\gamma (x) \gamma (y)}{\gamma (x + y)} \)

分布確率密度関数　:　\(\displaystyle f(p, a, b) = \frac{\gamma(a + b)}{\gamma(a)\gamma(b)}x^{a – 1}(1 – x)^{b -1} \)

これをこれま同様と同じ条件で計算してみる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma

def beta_distribution(p, a, b):
  """
  ガンマ関数によるベータ分布
  param p : 確率
  param a : 成功数
  param b : 失敗数
  return  : ベータ分布
  """
  result = (gamma(a + b) / gamma(a) * gamma(b)) * (p ** (a - 1)) * ((1 - p) ** (b - 1))
  return result

# 成功数
a = 20
# 失敗数
b = 80
t = np.linspace(0, 1, 100)  
plt.plot(t, beta_distribution(t, a, b), alpha=0.5)

同じグラフが出力された。