二項分布
コインを投げたときに表が出るのか、それとも裏が出るのか、といったように試行した際に起こる結果が2つしかない試行のことをベルヌーイ試行といい、このベルヌーイ試行をn回行い、表が出る回数の確率分布を二項分布という。グラフにすると正規分布に似たようなグラフになり、正規分布から二項分布に近似させることもできる。正規分布は、12.43653、13.54748765などといった細かく連続的な数値、すなわち連続型であるのに対し、二項分布はコインの試行のように10回、20回などのように決まった数値になる、すなわち離散型である。
\(\displaystyle \begin{pmatrix} n \\ k \end{pmatrix} = {}_n \mathrm{ C }_k = \frac{n!}{k!(n -k)!} \)
二項分布確率質量関数 : \(\displaystyle \begin{pmatrix} n \\ k \end{pmatrix} p^k (1 – p)^{n-k} \)
正規分布による近似 : \(\displaystyle \frac{1}{\sqrt{2 \pi np(1 – p)}} \exp \left( – \frac{(k – np) – 2}{2np(1 – p)} \right) \)
Pythonで二項分布を求める
とりあえず、二項分布の関数を作成し、グラフを描いてみる。
二項分布確率質量関数 : \(\displaystyle \begin{pmatrix} n \\ k \end{pmatrix} p^k (1 – p)^{n-k} \)
def binomial_distribution(n, k, p):
"""
二項分布
param n : n
param k : k
param p : 確率
return : 二項分布
"""
x = (p ** k) * ((1 - p) ** (n - k))
y = math.factorial(n) / (math.factorial(k) * math.factorial(n - k))
result = x * y
return result
n = 100
points = np.array([binomial_distribution(n, k, 0.5) for k in range(n + 1)])
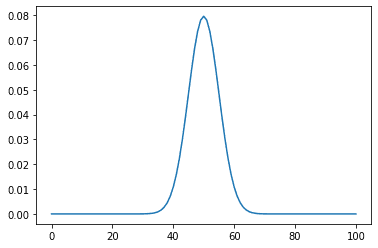
plt.plot(points)
正規分布のように左右対称の山のグラフが描かれた。次は、実際に二項分布により勝率を求めてみる。
NBAのプレイオフは16チームのトーナメント制で、7戦行い先に4勝した方が勝ち進んでいく7番勝負。16チームなので7勝負を4回勝ち進んで行けば優勝ということ。この確率を二項分布で表してみる。
まず、下記の組み合わせの式では、勝ち負けのパターンがわかる。
\(\displaystyle \begin{pmatrix} n \\ k \end{pmatrix} = {}_n \mathrm{ C }_k = \frac{n!}{k!(n -k)!} \)
\(\displaystyle \begin{pmatrix} 7 \\ 4 \end{pmatrix} = {}_7 \mathrm{ C }_5 = \frac{7!}{4!(7 -4)!} = \frac{7!}{4!(3)!} = 35 \)
import math
n = 7
k = 4
math.factorial(n) / (math.factorial(k) * math.factorial(n - k))35.0つまり、[勝, 勝, 勝, 勝, 勝, 勝, 勝]、[勝, 勝, 勝, 勝, 勝, 勝, 負]、[勝, 勝, 勝, 勝, 勝, 負, 負]、[勝, 勝, 勝, 勝, 負, 負, 負]、など7番勝負を勝つパターンが35個あるということ。
これを踏まえて、二項分布を求めてみる。
二項分布確率質量関数 : \(\displaystyle \begin{pmatrix} n \\ k \end{pmatrix} p^k (1 – p)^{n-k} \)
七番勝負の勝率は4〜7勝する確率の総和となる。また、リーグ戦の勝率が6割のチームの優勝する確率を求める。
import math
def binomial_distribution(k, n, p):
"""
二項分布
param k : k
param n : n
param p : 勝率
return : 二項分布
"""
# 組み合わせ
c = math.factorial(n) / (math.factorial(k) * math.factorial(n - k))
# 二項分布確率質量関数
result = c * (p ** k) * ((1 - p) ** (n - k))
return result
# チャンピオンになる確率
champion = 0
# 4~7勝する確率の総和
for i in range(4, 8):
champion += binomial_distribution(i, 7, 0.6)
print(champion)0.7102080000000001リーグ戦で勝率が6割のチームが優勝する確率は、0.71(71%)となった。
scipyでの二項分布
scipyではpmf関数で二項分布を実装できる。先程と同じ条件で二項分布を求めてみる。
from scipy.stats import binom
# チャンピオンになる確率
champion = 0
for i in range(4, 8):
champion += binom.pmf(i, 7, 0.6)
print(champion)0.7102080000000003同じような結果が出力された。
正規分布による近似
次に、正規分布から二項分布を近似させてみる。
正規分布による近似 : \(\displaystyle \frac{1}{\sqrt{2 \pi np(1 – p)}} \exp \left( – \frac{(k – np) – 2}{2np(1 – p)} \right) \)
import numpy as np
def log_normal_distribution(k, n, p):
"""
正規分布による二項分布への近似
param k : k
param n : n
param p : 勝率
return : 二項分布
"""
x = np.sqrt(2 * np.pi * n * p * (1 - p))
y1 = -1 * ((k - n * p) ** 2)
y2 = 2 * n * p * (1 - p)
result = (1 / x) * np.exp(y1 / y2)
return result
# チャンピオンになる確率
champion = 0
# 4~7勝する確率の総和
for i in range(4, 8):
champion += binomial_distribution(i, 7, 0.6)
print(champion)0.7102080000000001近似なので多少差異があるが同じような値が出力された。

記事を読んでいただきありがとうございました。